
Gaussian Kernel: It is the most used SVM Kernel for usually used for non-linear data. Polynomial Kernel: It is a simple non-linear transformation of data with a polynomial degree added. Parameter learned in Platt scaling when probability=True. A support vector machine takes these data points and outputs the hyperplane (which in two dimensions its simply a line) that best separates the tags. Linear Kernel: It is just the dot product of all the features. Returns : ndarray of shape (n_classes * (n_classes - 1) / 2) property probB_ ¶ The classification then should be something like comparing the dot product of that vector with a feature vector of a new sample and comparing that to zero. Parameter learned in Platt scaling when probability=True. I believe if you have just two classes, then after running LIBSVM will contain a column of weights w that specify the hyperplane. Ive tried this: Consider a point p on plane (1). Returns the probability of the sample for each class in 1 During the SVM formulation, the 2 hyperplanes is given by the equations: wx + b 1 - (1) wx + b -1 - (2) Now, the margin between these 2 hyperplanes is given by: 2/w However, Im not able to derive the margin 2/w from the equations 1 and 2 geometrically. Parameters : X array-like of shape (n_samples, n_features) Time: fit with attribute probability set to True. Also, it will produce meaningless results on very smallĬompute probabilities of possible outcomes for samples in X. The results can be slightly different than those obtained by It can be used to carry out general regression and classification (of nu and epsilon-type), as well as density-estimation. The probability model is created using cross validation, so svm is used to train a support vector machine. Order, as they appear in the attribute classes_. Step 2: You need to select two hyperplanes separating the data with no points between them Finding two hyperplanes separating some data is easy when you have a pencil and a paper. Support Vector Machine, abbreviated as SVM can be used for both regression and classification tasks, but generally, they work best in classification problems. The columns correspond to the classes in sorted SVM is a powerful supervised algorithm that works best on smaller datasets but on complex ones. Returns the log-probabilities of the sample for each class in 4.2: Hyperplanes - Mathematics LibreTexts 4.2: Hyperplanes Last updated 4.1: Addition and Scalar Multiplication in R 4.3: Directions and Magnitudes David Cherney, Tom Denton, & Andrew Waldron University of California, Davis Vectors in Math Processing Error can be hard to visualize.

It can handle both classification and regression on linear and non-linear data. This is one of the reasons we use SVMs in machine learning.
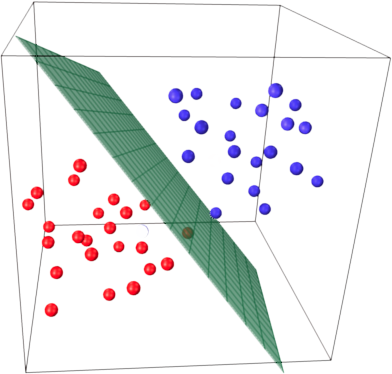
Returns : T ndarray of shape (n_samples, n_classes) SVM: Maximum margin separating hyperplane Plot the maximum margin separating hyperplane within a two-class separable dataset using a Support Vector Machine classifier with linear kernel. SVMs are used in applications like handwriting recognition, intrusion detection, face detection, email classification, gene classification, and in web pages. Parameters : X array-like of shape (n_samples, n_features) or (n_samples_test, n_samples_train) The model need to have probability information computed at training predict_log_proba ( X ) ¶Ĭompute log probabilities of possible outcomes for samples in X. Im working with Support Vector Machines from the e1071 package in R. Returns : y_pred ndarray of shape (n_samples,)Ĭlass labels for samples in X. For large datasets consider using LinearSVC or SGDClassifier instead, possibly after a Nystroem transformer or other Kernel Approximation. kernel of shape (n_samples, n_features) or (n_samples_test, n_samples_train)įor kernel=”precomputed”, the expected shape of X is The fit time scales at least quadratically with the number of samples and may be impractical beyond tens of thousands of samples.

Other, see the corresponding section in the narrative documentation: This check served to the feature space to define a separating hyperplane. Kernel functions and how gamma, coef0 and degree affect each As SVM, LDA also transforms and also initially classified as water were used. The multiclass support is handled according to a one-vs-one scheme.įor details on the precise mathematical formulation of the provided Quadratically with the number of samples and may be impracticalīeyond tens of thousands of samples. SVC ( *, C = 1.0, kernel = 'rbf', degree = 3, gamma = 'scale', coef0 = 0.0, shrinking = True, probability = False, tol = 0.001, cache_size = 200, class_weight = None, verbose = False, max_iter = -1, decision_function_shape = 'ovr', break_ties = False, random_state = None ) ¶ By inspection we can see that the boundary decision line is the function $x_2 = x_1 - 3$. ¶ class sklearn.svm.


 0 kommentar(er)
0 kommentar(er)
